La conversion analogique-numérique repose sur deux opérations fondamentales que sont l’échantillonnage et la quantification.

- L’échantillonnage consiste à prélever des petits échantillons de son (ce qui revient à mesurer des différences de pression) à des intervalles de temps précis. L’intervalle de temps entre deux échantillons est appelé fréquence d’échantillonnage ou encore taux d’échantillonnage. Le nombre d’échantillon par seconde s’exprime en Hertz (Hz). La fréquence d’échantillonnage est un paramètre très important de l’échantillonnage car elle définit la qualité de l’enregistrement. En effet, plus la fréquence d’échantillonnage est élevée, plus l’intervalle de temps entre chaque échantillon est faible et donc plus fidèle sera le signal final au signal initial. Par contre il est évident que plus la fréquence d’échantillonnage sera élevée, plus le nombre de donnés à stocker est importante donc plus le signal nécessitera une mémoire importante. Le théorème de Nyquist-Shannon stipule que cette fréquence doit être égale ou supérieure à deux fois la fréquence maximale du signal afin que le signal ne soit pas perturbé par l’échantillonnage. Ce théorème a permis de mettre au point une fréquence standard : sachant que l’oreille humaine ne perçoit les sons que jusqu’à une fréquence d’environ 20 kHz, la fréquence d’échantillonnage doit être supérieur ou égal à 40kHz, la valeur précise de 44.1kHz a été choisie comme standard. Elle provient des contraintes de synchronisation avec les équipements vidéo. Ceci permet de ne pas  traiter les sons inaudibles qui ne présenteraient aucun avantage pour une écoute humaine ultérieure du signal échantillonnée.

- La deuxième opération, la quantification, consiste à remplacer les valeurs exactes analogiques de l’échantillon par la plus proche valeur binaire possible. Donc à chaque échantillon est associé un nombre binaire. Ce dernier détermine la valeur approximative de la pression du fluide de propagation (de l’air, en règle générale), à un instant donné. Le son n’est plus représenté par une courbe continue mais par une suite de valeurs discrètes sur chaque intervalle de temps. La quantification est caractérisée par un paramètre nommé résolution. Il détermine le nombre de valeurs différentes qu’un échantillon peut prendre, aussi appelé nombre de bits. De même que pour la fréquence d’échantillonnage, plus la résolution est élevée, plus grande est la qualité de l’information et le besoin en mémoire, ainsi que le prix du composant est élevé. Avec un nombre de bits x on a 2^x possibilités de valeurs. Par exemple un signal de 16 bits (2 octets) va donner 2¹⁶ possibilités de solutions différentes, ce qui va permettre de coder le niveau du signal entre -32767 et 32768. Le choix du nombre de bits du convertisseur va conditionner aussi l’étendu du signal que l’on peut capter. A 1 kHz la plus petite variation de pression détectable par l’oreille humaine est de 2 x 10^-5 Pa, si l’on attribue à cette variation de pression la valeur de 1 du convertisseur analogique sélectionné. Pour un convertisseur 16 bits alors la valeur maximale de 32768 correspond à un son d’intensité relative de 90 dB soit le niveau sonore d’un orchestre symphonique. Pour un convertisseur 24 bits le signal peut être codé entre -8388607 et 8388608. La valeur de 8388608 correspond à un son d’intensité relative de 138,5 dB soit un niveau sonore correspondant au seuil de l’intolérance. Le seuil intolérable du système auditif humain est compris entre 130 dB et 140 dB. A l’enregistrement bien qu’un convertisseur 16 bits soit suffisant généralement on travaille à des résolutions supérieures (20,24, voir 32 bits) pour avoir une plage de manœuvre plus importante. Numériser à haute résolution permet de garder une qualité optimum.

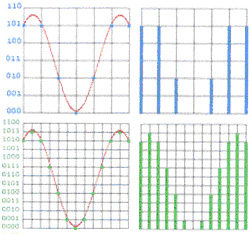
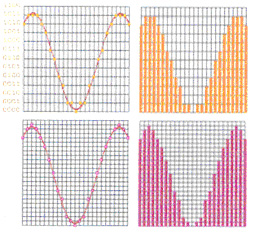
Figure 2 : Evolution de l’échantillonnage en fonction de la fréquence et de la résolution.